What are Neuro-Sounds?
 Neuro-Sounds are tones based on any fundamental frequency that are in harmonic proportion to one another.
Neuro-Sounds are tones based on any fundamental frequency that are in harmonic proportion to one another.
If you are new to the concept of harmonics, you can begin by learning to calculate the mathematics of overtone ratios. This will teach you the physics of sound and the principles of feedback resonance. By understanding the sounds through both your cortex and your body, you are learning to navigate a developmental model of resonance. As you progress, you will be able to compose and design your own sound patterns and bio-music that is specifically attuned to you, your family, your home/office or your clients.
What is an Overtone?
If you strike a sound and listen closely, you will hear other tones emerge from the resonance (called “overtones”) that are different from the first one (called the “fundamental.”) Nature organizes these overtones into a series of predictable ratios. No matter what fundamental you start on, the series of overtones will always unfold in the same mathematical way. Differences in sound are measured by counting the number of vibrations per second (hertz.) The overtone series generated from a fundamental is called “the harmonic series”, “harmonics”, “partials” or “integer frequency ratios.”
Depending on one’s culture, sounds that match overtone proportions are usually heard as consonant and thus the most “musical.” When sounds fall in the “cracks” between overtone ratios or get too distant from the fundamental, they can sound disturbing or dissonant.
Here is a chart showing you the mathematical ratios of an overtone series.
Mathematical Proportions of the Overtone Series
(Based Upon a Starting Fundamental of 55 Hz)

Try filling in the mathematical blanks using the above ratios when you start on a fundamental frequency of 65 Hz (the note C.)
1:1 Fundamental: 65 Hz C
2:1 Octave: 110 Hz
3:2 Fifth: 195 Hz
4:3 Fourth: 260 Hz
5:4 Major third: 325 Hz
6:5 Minor third: 390 Hz
7:6 Minor third: 455 Hz
8:7 Major second: 520 Hz
Note: Numbers are often rounded off to the nearest whole number.
Here’s how the musical notes would look if the overtone ratios were notated on sheet music based upon the first example of a fundamental of 55 Hz.
Mathematical Proportions of the Overtone Series in Musical Notes
(Based upon the Fundamental of A 55 Hz)

Click to hear how these overtone ratios sound if you played them on a piano
The overtone series continues indefinitely and generates all possible frequencies. It is occurring even with natural phenomena we can’t hear. For instance, atomic particles have been found to vibrate to the ratios of the overtone series. (See Links for reference.)
Click below to listen to each ratio separately and experience its resonance. In this chart, the fundamental (A 55 Hz) is presented with its first seven overtones. Listen to the overtones in order as this is the best way to learn how they relate to one another.
- Fundamental 55 Hz (A)
- 1st Overtone Octave 110 Hz
- 2nd Overtone Fifth 165 Hz
- 3rd Overtone Fourth 220 Hz
- 4th Overtone Major 3rd 277 Hz
- 5th Overtone Minor 3rd 329 Hz
- 6th Overtone Minor 3rd 392 Hz
- 7th Overtone Major 2nd 440 Hz
If you would like to build your own harmonic protocol, some basic choices and ideas are presented below.
- Choose a fundamental you would like to work with from the chart below entitled Fundamentals and their First Seven Overtones. (For example, the note A.) The fundamental and its first seven overtones are the notes you will be using in your exercise. Tones are listed in the mathematical order in which they unfold. The fundamental is usually sounded first. It’s best to use to overtones in sequential order at first so that the brain learns the progression. Then they can be used in any order.
Fundamentals and their First Seven Overtones
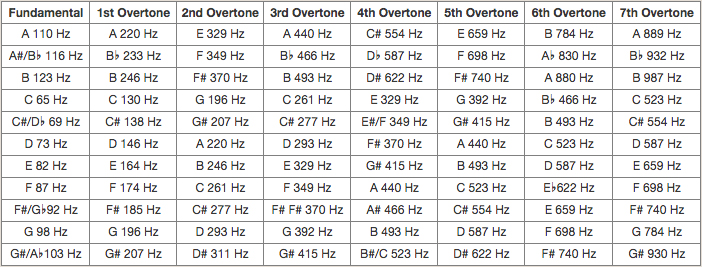
- Choose the octave range you would like to use. (Higher range usually is good for focus, lower range for relaxation. Here are two charts to guide you—the first to help you choose an octave range and the second to help you hop around different octave ranges mathematically.
Range of Low to High Frequencies (Middle C on the piano is 261 Hz)
Mathematical Ratios of Octaves Based on Different Musical Notes Measured in Hertz (Hz)

- Decide what kind of durations you need for the sounds in the protocol. Short sounds are good for immediate acknowledgement that the goal has been achieved and long sounds are good for pauses between sets or consolidation periods. (Short and long sounds can be combined in the same protocol.)
- If you are uncertain what to choose, here is a basic example:
(Piano) Fundamental of C:
- 261 Hz (short) immediate reinforcement tone
- 131 Hz (short) for use after a certain number of goals are achieved
- 66 Hz (long) during pause between exercises
- 131 Hz Overtone series (long) for closing eyes after exercise and consolidating
Or
131 Hz Cycle of 5ths (long) for closing eyes after exercise and consolidating
Historical use of overtones
Overtones have a long history in healing and therapy. The power of the overtone series was well understood by the Greeks who healed with sound and constructed their buildings to overtone proportions. (This created a “resonant house” and the feeling of awe we get in certain cathedrals—see link for Sacred Geometry.) Today, principles of resonance underlie many of our medical treatments and assessment procedures. (See link for International Association of Music and Medicine.)
Psychology of Overtones
Overtones are symbolic of a structural “gateway” for consciousness potential. When monks chant on one fundamental tone, their voices naturally produce overtones that vibrate our bodies, brains and the walls of the room we’re sitting in. If we think of the overtone series symbolically, the fundamental is the foundation from which everything grows. The first overtone after the fundamental is the octave—the closest reflection of the fundamental itself and thus the most powerful tone for grounding and inspiration. The 2nd overtone is the fifth—the first time the fundamental differentiates into something other than itself—like a birth. The 3rd overtone is a new proportion (the fourth) but is the same sound as the fundamental two octaves higher—like the last reflection of the parent before individuating into the world.
How Can We Use Overtones Therapeutically?
Overtone sounds provide an excellent opportunity to work at a proportional level with the body and brain. This means that harmonic proportion is created between different frequencies so that the proportion itself generates a therapeutic effect (e.g., between sound and frequencies of the body or doorbell and cellphone.)
Because overtones reflect nature’s structure exactly, they create a resonant holding environment for health, development and growth. They can also be used to balance, harmonize, activate, sedate, deepen, expand, align or stimulate.
Overtones activate network dynamics that connect circuits at different levels of the organism. Every sound functions in a complex way and generates a resonance effect at multiple levels. For instance, the note A (440 Hz) can act as the fundamental of its own series at the same time as it functions as an overtone in another series. (This is where use of the Library requires more training.)
Many frequencies, including those of the brain, heart and organs of the body, cannot be heard because they fall above or below the 20-20,000 Hz human hearing range. (See Links for more information.) We can still work with them, however, because the principle of harmonics allows us to conceptualize relational proportions mathematically.
Dr. Lemare-Calaba uses the Library of Sounds to create harmonic proportions between brainwave frequencies and sound. Other therapeutic applications include mirroring a client’s tone of pain or joy, aligning with a frequency of relaxation or focus, discerning what frequencies a person’s body prefers, harmonizing the vibrations of a room or designing personalized tone sequences.
Can we use frequencies that fall between the overtone numbers?
Frequencies that fall in the “cracks” between overtone ratios may sound “off key” or dissonant if you are using them in combination with other musical ratios. This would be like improvising and returning to the “home” of a stable overtone ratio. These frequencies would be identified by their numbers rather than a musical name. (For the music theorist, musical proportions can be organized around any chosen tuning system. Concert A is currently 440 Hz, but if we made it 434 Hz and all the numbers would change.)
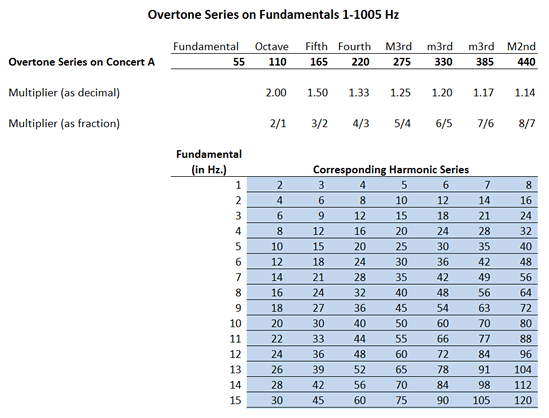
Just in case you are interested in venturing out of the current 440 Hz tuning structure and inventing your own tuning system, harmonic ratios are printed out on every frequency from 1-1005 Hz on the chart below. The numbers may have to be adjusted slightly if you wish to accommodate specific tuning systems (e.g. equal temperament.)
Mathematical Proportions of Overtone Series Based on Fundamentals from 1-1005 Hz. Click Image to See the Complete Chart
Library of Musical Overtone Sounds
Dr. Lemare Calaba uses her own Library of Musical Overtone Sounds for Piano to create harmonic protocols. This library consists of a collection of acoustic piano tones and tone sequences recorded on 88 keys of a Kawai piano. Each tone was professional engineered to capture a maximum amount of overtone resonance.
The collection is organized by note name so that custom protocols can be designed and preferences can be chosen from a menu. For instance, the note A has options for: a) short tones; b) long resonant tones; c) notes in different octaves; d) notes in overtone ratios of the fundamental; e) intervals and chords; and f) tone sequences (e.g., overtone series and circled of fifths).
To master Musical Overtone Feedback or the art of building your own harmonic protocols, feel free to arrange a consultation with Dr. Calaba or host a Neuro-Sound workshop in your home town.
If you are interested in inquiring about purchase of the Library of Musical Overtone Sounds, please contact Dr. Lemare-Calaba.

